- Μηνύματα
- 385
- Πόντοι
- 16
TEMPERAMENTS
Τολμώ και παρουσιάζω , σαν Ηλεκτρονικός Μηχανικός που έχει και μερικές γνώσεις της μουσικής θεωρίας, ένα πολύ δύσκολο θέμα-τους ‘’συγκερασμούς’’.
Όλες οι πληροφορίες αντλήθηκαν από εξαντλητικές ερωτήσεις σ’ ένα ξένο site (slidemeister.com με το οποίο συνεργάζομαι) στo οποία ξεκίνησα να περιγράφω τον παρακάτω πρακτικό τρόπο κουρδίσματος μιας φυσαρμόνικα . Βλέπε το video μου ΕΔΩ:
Μετά διαπίστωσα ότι συνδυάζοντας και την πολύ πλούσια θεωρία που υπάρχει για το θέμα, θα καταλάβαινα πολύ καλύτερα τη διαδικασία κουρντίσματος.
Φυσικά δεν είμαι συγγραφέας και έτσι πολλά από τη θεωρία ίσως επαναλαμβάνονται με εμπλουτισμένο υλικό που έπαιρνα κάθε φορά καθώς μου δημιουργούνταν νέες ερωτήσεις.
Επειδή το θέμα των Temperaments είναι ανοιχτό προς εξερεύνηση εγώ απλώς προσπάθησα εκτός από την εντελώς ΠΡΑΚΤΙΚΗ διαδικασία κουρντίσματος των φυσαρμόνικων να δώσω και μια ευκαιρία σε πολλούς από εσάς που έχετε πανεπιστημιακές μουσικές γνώσεις , να το συζητήσουμε και να εμπλουτίσουμε περαιτέρω τις γνώσεις μας.
Το ότι στις επόμενες ενότητες που θα ακολουθήσουν, τα παραδείγματα αναφέρονται στις φυσαρμόνικες δεν θα σας εμποδίσει να εμπλουτίσετε τις γνώσεις σας αλλά και να κάνετε αναγωγή στο δικό σας όργανο.
Θεώρησα σωστό, για την καλύτερη κατανόηση, να περιγράψω περιληπτικά και μερικά αξιώματα της φυσικής.
Για καλύτερη μελέτη καλόν θα ήταν οι αρκετές περιγραφικές σελίδες μου με τα σχεδιαγράμματα, που δίνω μέσω των links, να εκτυπωθούν και να μελετώνται ταυτόχρονα με το παρόν κείμενο.
Γενικά για το κούρδισμα:
Υπάρχουν πολλοί τρόποι για το πώς οι οργανοπαίχτες θα πρέπει να κουρδίζουν τα όργανα τους ώστε να παίζουν συντονισμένα.
Πάντως ένα είναι γεγονός το ότι αν ένας οργανοπαίχτης πρόκειται να συμμετάσχει σε μια ομάδα μουσικών, ακόμα και μόνο με άλλον ένα, θα πρέπει να γνωρίζει να βαθμονομεί το όργανό του ώστε να είναι σε συντονισμό με αυτά της ομάδας.
Συχνότητα και ακουστικά διακροτήματα (beats)
“Intonation without beats is the goal of all musicians.”
Δηλαδή σκοπός των μουσικών είναι να επιτύχουν τέτοιο κούρδισμα ώστε να μη υπάρχουν διακροτήματα (beatless).
Κάθε ακουστικό κύμα έχει μια μετρήσιμη ταχύτητα συνεχόμενης κίνησης που λέγεται συχνότητα και μετριέται σε κύκλους /δευτερόλεπτο ή Hertz και την αντιλαμβανόμαστε σαν τόνο.
Όσο ταχύτερη η ταχύτητα τόσο ο τόνος που αντιλαμβανόμαστε είναι ψηλότερος.
Όταν ήχοι από δύο διαφορετικές πηγές συνδυαστούν στον αέρα τότε ο ένας επικάθεται επί του άλλου και ο προκύπτον τόνος είναι είτε χαμηλότερος είτε υψηλότερος σε ένταση.
Δύο τόνοι που ηχούν στην ίδια συχνότητα συνδυάζονται και δυναμώνεται η ένταση τους.
Δύο τόνοι με ελαφρώς διαφορετικές συχνότητες παράγουν το λεγόμενο διακρότημα (beat) που είναι ένας τόνος που ακούγεται μη σταθερός (wa-wa).
Για να μπορούν οι οργανοπαίχτες να παίζουν σε συντονισμό πρέπει να προσαρμόζουν τον τόνο του οργάνου τους με τον τόνο μιας αξιόπιστης πηγής τόνων.
Για να συγκρίνει ο οργανοπαίχτης τον τόνο του οργάνου του με τον τόνο της αξιόπιστης πηγής τόνων ακούει το διακρότημα:
• Όσο πιο ταχύτερο τόσο ασύμφωνοι είναι.
• Οταν οι τόνοι του οργάνου και της αξιόπιστης πηγής πλησιάζουν σε συχνότητα τότε το διακρότημα ηχεί αργότερο
• και όταν οι συχνότητες συμπέσουν τότε ένας σταθερός, ενδυναμωμένος τόνος ηχεί που μοιάζει με έναν τόνο παρά με συνδυασμό δύο.
Αρμονικές Συχνότητες
Kάθε νότα που παράγεται από ένα μουσικό όργανο έχει συνιστώσες που αποτελούνται πάντα από τη βασική της συχνότητα και μέχρι κάποιο όριο όλα ή ορισμένα από τα ακέραια πολλαπλάσιά της (διπλάσια, τριπλάσια κτλ).
Οι συνιστώσες αυτές ονομάζονται αρμονικές– η πρώτη λέγεται και θεμελιώδης.
Το διάστημα που σχηματίζουν δύο φθόγγοι εκφράζεται με το λόγο των συχνοτήτων τους. Έτσι, επειδή από κάθε αρμονική στην επόμενη οι λόγοι των συχνοτήτων μικραίνουν (1/2, 2/3, ….), ανάλογα μικραίνουν και τα διαστήματα μεταξύ τους.
Οι λόγοι αυτοί είναι το μέτρο των διαστημάτων (π.χ. 2/1 = οκτάβα, 3/2 = καθαρή πέμπτη, 5/4 = μεγάλη τρίτη, 3/1 = δωδεκάτη).
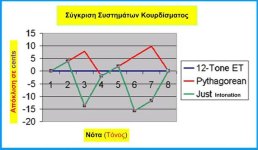
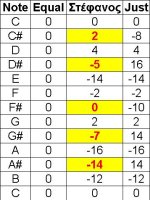
Αν έχουμε οποιαδήποτε απόκλιση από το μέτρο αυτό τότε αυτό λέγεται συγκερασμός (Temperament).
Tο ισοσυγκερασμένο σύστημα (Equal Temperament = E.T) σημαίνει την υποδιαίρεση της οκτάβας σε 12 ίσα ημιτόνια.
Άρα όλα τα άλλα διαστήματα προκύπτουν ως το άθροισμα του κατάλληλου αριθμού τέτοιων ημιτονίων (καθαρή Τετάρτη=7 ημιτόνια, καθαρή πέμπτη = 7 ημιτόνια, μεγάλη τρίτη = 4 ημιτόνια ….).
Στο Ε.Τ ισχύει και η εναρμόνια ισοδυναμία, όπου π.χ C# =Db, αφού η απόσταση από το C και το D είναι ίση.
Δείτε τη φωτογραφία ΕΔΩ:
http://www.box.net/shared/3snhxq50jfinrgy4zy6z
Το ψηφιακό χρωματικό tuner{κουρδιστήρι}
Είναι σύνηθες να βασιζόμαστε στο Tuner για το κούρδισμα του οργάνου μας.
Το Tuner δείχνει πόσα cents απέχει ο τόνος που παίζεται από έναν τόνο μιας αξιόπιστης ακουστικής πηγής.
Αυτό μπορεί να είναι χρήσιμο σε ένα σταθερού σωλήνα πνευστό όργανο (σάλπιγγα) ή για το συντονισμό της χορδής Α (λά) στα έγχορδα.
Πάντως δεν θα πρέπει να χρησιμοποιείται το tuner για κούρδισμα όλων των χορδών εγχόρδων {φημισμένοι κιθαρίστες κουρδίζουν τις υπόλοιπες χορδές στηριζόμενοι στο αυτί τους} ή για όλες τις οκτάβες για τα πνευστά (κλαρίνο, σαξόφωνο, φλάουτο..)..
Αυτό οφείλεται στο ακουστικό φαινόμενο που συμβαίνει με τα just-tempered συστήματα που θα μελετήσουμε στη συνέχεια.
CENTS
Cents είναι μία λογαριθμική μονάδα ίση με το 1/ 1200 μιας
(π.χ. 1 οκτάβα = 1200 cents ,1 ημιτόνιο = 100 cents, 1Πέμπτη =7ημιτόνια = 700
Cents ……),
Πρόσθεση διαστημάτων
Πχ 1 Τετάρτη ( 500 cents) + 1 πέμπτη (700 cents) = 1200 cents = 1 οκτάβα ή το ίδιο 1 ογδόη
Κούρδισμα Equal Tempered { ισοσυγκερασμένο κούρδισμα}
Το ενδιαφέρον πρόβλημα του κουρδίσματος το αντιμετώπισαν για εκατοντάδες χρόνια οι κατασκευαστές οργάνων .
Tο ισοσυγκερασμένο κούρδισμα είναι γνωστό από το 16ο αιώνα αλλά επιβλήθηκε το 19ο αιώνα.
Tα προβλήματα των κουρδισμάτων αφορούν περισσότερο τα πληκτροφόρα, οι μουσικοί των οποίων δεν μπορούν να επέμβουν στο ακριβές τονικό ύψος κάθε νότας.
Έτσι για να πάρουμε την καθαρή πέμπτη (το διάστημα μεταξύ Α και Ε) πρέπει να πολλαπλασιάσουμε 1,5 φορά τη συχνότητα της Α.
Στο βιολί (τη βιόλα ,τη λύρα αλλά και σ’ όλα τα χωρίς τα έγχορδα χωρίς χωρίσματα-όπως τα χωρίσματα-frets- της κιθάρας)αυτό είναι δυνατόν και μπορούμε να παίξουμε την καθαρή πέμπτη Ε στη συχνότητα 440Χ1,5=660 Hz.
Από τον παρακάτω όμως πίνακα συχνοτήτων βλέπουμε ότι το πιάνο παίζει την ίδια νότα Ε = 659.26 Hz δηλαδή να βαίνει προς ύφεση.
{ Αυτό οφείλεται στον κούρδισμα equal tempered. Λέγεται ότι το κούρδισμα αυτό επινοήθηκε ή ότι καθιερώθηκε την εποχή του Bach και πως ο Bach το προτιμούσε και το επέβαλε ή ότι βοήθησε στην καθιέρωσή του. Άλλοι λένε αυτό δεν ευσταθεί και είναι παρεξήγηση….}.
Στο Ε.Τ η οκτάβα χωρίζεται σε δώδεκα ίσα τμήματα, καθένα από τα οποία είναι “κατά προσέγγιση ένα ημιτόνιο” (λέμε κατά προσέγγιση, διότι το πραγματικό ημιτόνιο δεν είναι το ένα δωδέκατο της οκτάβας). Σύμφωνα με τον Kirnberger (μαθητή του Bach) “ο ισοσυγκερασμός δεν εξασφαλίζει την ποικιλομορφία των τονικοτήτων.
Αυτό σημαίνει ότι όλα τα παραπάνω αναφερθέντα έγχορδα πρέπει να υπακούουν σ’ αυτές τις ελαφρές διαφορές κατά τα κουρδίσματα με το πιάνο.
Οι οργανοπαίχτες αυτών των οργάνων αισθάνονται πιο ‘ευτυχείς’ όταν παίζουν μόνο με άλλα τέτοια έγχορδα.
Για καλύτερη κατανόηση του παραπάνω πίνακα συχνοτήτων δείτε ΕΔΩ:
http://www.box.net/shared/6acbbehivova368faga0
Συχνότητες των τόνων
Οι συχνότητες των τόνων βρίσκονται από τον μαθηματικό τύπο:
Συχνότητα: f= 440×12η ρίζα του 2 εις την x δύναμη
Όπου x = -21, -19, ..., 27. (το πρόσημο είναι + για πάνω από τη Α4 και – για κάτω από τη Α4). (αν αναφερόμαστε για την 1η οκτάβα ,όπως στο ανωτέρω link τότε χ=12)
Δείτε την ονομασία και τις συχνότητες των οκτάβων ΕΔΩ:
http://www.box.net/shared/yum71z5jidjjqmhesdm9
Παράδειγμα 1ον:Ποια είναι η συχνότητα του C5;
Το C5 είναι το πρώτο C πάνω από τη Α4. Ανάμεσα στο Α4 και στο C5 υπάρχουν 3 ημιτόνια (Α4 Α#4 Β4 C5 ) και η C5 πάνω από τη A4. Άρα n=+3.Αποτέλεσμα f=523,2 Hz
Παράδειγμα 2ον: Ποια είναι η συχνότητα του F4;
Το F4 είναι κάτω από το A4. Ανάμεσα στο Α4 και στο F4 υπάρχουν 4 ημιτόνια ( A4 Ab4G4Gb4F4) και άρα n=-4
Αποτέλεσμα f=349,2 Hz:
Τον πίνακα με όλες τις συχνότητες δείτε τον ΕΔΩ:
http://www.box.net/shared/gvkohn0e9d2ggas66vag
Από τον πίνακα φαίνεται ότι η οκτάβα χωρίστηκε σε 12 ίσα διαστήματα με την πρώτη και την τελευταία νότα να έχουν λόγο συχνοτήτων 2 και άρα να δίνουν το ίδιο τονικό ύψος σε διαδοχικές οκτάβες.
Εδώ : http://www.contrabass.com/pages/frequency.html
θα δείτε έναν ενδιαφέροντα πίνακα με τις νότες από C2 έως C6 τις συχνότητες τους , την περιοχή τους στα μουσικά όργανα και links σε όλα τα μουσικά όργανα για περισσότερες πληροφορίες.
Συνεχίζεται...
Τολμώ και παρουσιάζω , σαν Ηλεκτρονικός Μηχανικός που έχει και μερικές γνώσεις της μουσικής θεωρίας, ένα πολύ δύσκολο θέμα-τους ‘’συγκερασμούς’’.
Όλες οι πληροφορίες αντλήθηκαν από εξαντλητικές ερωτήσεις σ’ ένα ξένο site (slidemeister.com με το οποίο συνεργάζομαι) στo οποία ξεκίνησα να περιγράφω τον παρακάτω πρακτικό τρόπο κουρδίσματος μιας φυσαρμόνικα . Βλέπε το video μου ΕΔΩ:
Μετά διαπίστωσα ότι συνδυάζοντας και την πολύ πλούσια θεωρία που υπάρχει για το θέμα, θα καταλάβαινα πολύ καλύτερα τη διαδικασία κουρντίσματος.
Φυσικά δεν είμαι συγγραφέας και έτσι πολλά από τη θεωρία ίσως επαναλαμβάνονται με εμπλουτισμένο υλικό που έπαιρνα κάθε φορά καθώς μου δημιουργούνταν νέες ερωτήσεις.
Επειδή το θέμα των Temperaments είναι ανοιχτό προς εξερεύνηση εγώ απλώς προσπάθησα εκτός από την εντελώς ΠΡΑΚΤΙΚΗ διαδικασία κουρντίσματος των φυσαρμόνικων να δώσω και μια ευκαιρία σε πολλούς από εσάς που έχετε πανεπιστημιακές μουσικές γνώσεις , να το συζητήσουμε και να εμπλουτίσουμε περαιτέρω τις γνώσεις μας.
Το ότι στις επόμενες ενότητες που θα ακολουθήσουν, τα παραδείγματα αναφέρονται στις φυσαρμόνικες δεν θα σας εμποδίσει να εμπλουτίσετε τις γνώσεις σας αλλά και να κάνετε αναγωγή στο δικό σας όργανο.
Θεώρησα σωστό, για την καλύτερη κατανόηση, να περιγράψω περιληπτικά και μερικά αξιώματα της φυσικής.
Για καλύτερη μελέτη καλόν θα ήταν οι αρκετές περιγραφικές σελίδες μου με τα σχεδιαγράμματα, που δίνω μέσω των links, να εκτυπωθούν και να μελετώνται ταυτόχρονα με το παρόν κείμενο.
Γενικά για το κούρδισμα:
Υπάρχουν πολλοί τρόποι για το πώς οι οργανοπαίχτες θα πρέπει να κουρδίζουν τα όργανα τους ώστε να παίζουν συντονισμένα.
Πάντως ένα είναι γεγονός το ότι αν ένας οργανοπαίχτης πρόκειται να συμμετάσχει σε μια ομάδα μουσικών, ακόμα και μόνο με άλλον ένα, θα πρέπει να γνωρίζει να βαθμονομεί το όργανό του ώστε να είναι σε συντονισμό με αυτά της ομάδας.
Συχνότητα και ακουστικά διακροτήματα (beats)
“Intonation without beats is the goal of all musicians.”
Δηλαδή σκοπός των μουσικών είναι να επιτύχουν τέτοιο κούρδισμα ώστε να μη υπάρχουν διακροτήματα (beatless).
Κάθε ακουστικό κύμα έχει μια μετρήσιμη ταχύτητα συνεχόμενης κίνησης που λέγεται συχνότητα και μετριέται σε κύκλους /δευτερόλεπτο ή Hertz και την αντιλαμβανόμαστε σαν τόνο.
Όσο ταχύτερη η ταχύτητα τόσο ο τόνος που αντιλαμβανόμαστε είναι ψηλότερος.
Όταν ήχοι από δύο διαφορετικές πηγές συνδυαστούν στον αέρα τότε ο ένας επικάθεται επί του άλλου και ο προκύπτον τόνος είναι είτε χαμηλότερος είτε υψηλότερος σε ένταση.
Δύο τόνοι που ηχούν στην ίδια συχνότητα συνδυάζονται και δυναμώνεται η ένταση τους.
Δύο τόνοι με ελαφρώς διαφορετικές συχνότητες παράγουν το λεγόμενο διακρότημα (beat) που είναι ένας τόνος που ακούγεται μη σταθερός (wa-wa).
Για να μπορούν οι οργανοπαίχτες να παίζουν σε συντονισμό πρέπει να προσαρμόζουν τον τόνο του οργάνου τους με τον τόνο μιας αξιόπιστης πηγής τόνων.
Για να συγκρίνει ο οργανοπαίχτης τον τόνο του οργάνου του με τον τόνο της αξιόπιστης πηγής τόνων ακούει το διακρότημα:
• Όσο πιο ταχύτερο τόσο ασύμφωνοι είναι.
• Οταν οι τόνοι του οργάνου και της αξιόπιστης πηγής πλησιάζουν σε συχνότητα τότε το διακρότημα ηχεί αργότερο
• και όταν οι συχνότητες συμπέσουν τότε ένας σταθερός, ενδυναμωμένος τόνος ηχεί που μοιάζει με έναν τόνο παρά με συνδυασμό δύο.
Αρμονικές Συχνότητες
Kάθε νότα που παράγεται από ένα μουσικό όργανο έχει συνιστώσες που αποτελούνται πάντα από τη βασική της συχνότητα και μέχρι κάποιο όριο όλα ή ορισμένα από τα ακέραια πολλαπλάσιά της (διπλάσια, τριπλάσια κτλ).
Οι συνιστώσες αυτές ονομάζονται αρμονικές– η πρώτη λέγεται και θεμελιώδης.
Το διάστημα που σχηματίζουν δύο φθόγγοι εκφράζεται με το λόγο των συχνοτήτων τους. Έτσι, επειδή από κάθε αρμονική στην επόμενη οι λόγοι των συχνοτήτων μικραίνουν (1/2, 2/3, ….), ανάλογα μικραίνουν και τα διαστήματα μεταξύ τους.
Οι λόγοι αυτοί είναι το μέτρο των διαστημάτων (π.χ. 2/1 = οκτάβα, 3/2 = καθαρή πέμπτη, 5/4 = μεγάλη τρίτη, 3/1 = δωδεκάτη).
Αν έχουμε οποιαδήποτε απόκλιση από το μέτρο αυτό τότε αυτό λέγεται συγκερασμός (Temperament).
Tο ισοσυγκερασμένο σύστημα (Equal Temperament = E.T) σημαίνει την υποδιαίρεση της οκτάβας σε 12 ίσα ημιτόνια.
Άρα όλα τα άλλα διαστήματα προκύπτουν ως το άθροισμα του κατάλληλου αριθμού τέτοιων ημιτονίων (καθαρή Τετάρτη=7 ημιτόνια, καθαρή πέμπτη = 7 ημιτόνια, μεγάλη τρίτη = 4 ημιτόνια ….).
Στο Ε.Τ ισχύει και η εναρμόνια ισοδυναμία, όπου π.χ C# =Db, αφού η απόσταση από το C και το D είναι ίση.
Δείτε τη φωτογραφία ΕΔΩ:
http://www.box.net/shared/3snhxq50jfinrgy4zy6z
Το ψηφιακό χρωματικό tuner{κουρδιστήρι}
Είναι σύνηθες να βασιζόμαστε στο Tuner για το κούρδισμα του οργάνου μας.
Το Tuner δείχνει πόσα cents απέχει ο τόνος που παίζεται από έναν τόνο μιας αξιόπιστης ακουστικής πηγής.
Αυτό μπορεί να είναι χρήσιμο σε ένα σταθερού σωλήνα πνευστό όργανο (σάλπιγγα) ή για το συντονισμό της χορδής Α (λά) στα έγχορδα.
Πάντως δεν θα πρέπει να χρησιμοποιείται το tuner για κούρδισμα όλων των χορδών εγχόρδων {φημισμένοι κιθαρίστες κουρδίζουν τις υπόλοιπες χορδές στηριζόμενοι στο αυτί τους} ή για όλες τις οκτάβες για τα πνευστά (κλαρίνο, σαξόφωνο, φλάουτο..)..
Αυτό οφείλεται στο ακουστικό φαινόμενο που συμβαίνει με τα just-tempered συστήματα που θα μελετήσουμε στη συνέχεια.
CENTS
Cents είναι μία λογαριθμική μονάδα ίση με το 1/ 1200 μιας
(π.χ. 1 οκτάβα = 1200 cents ,1 ημιτόνιο = 100 cents, 1Πέμπτη =7ημιτόνια = 700
Cents ……),
Πρόσθεση διαστημάτων
Πχ 1 Τετάρτη ( 500 cents) + 1 πέμπτη (700 cents) = 1200 cents = 1 οκτάβα ή το ίδιο 1 ογδόη
Κούρδισμα Equal Tempered { ισοσυγκερασμένο κούρδισμα}
Το ενδιαφέρον πρόβλημα του κουρδίσματος το αντιμετώπισαν για εκατοντάδες χρόνια οι κατασκευαστές οργάνων .
Tο ισοσυγκερασμένο κούρδισμα είναι γνωστό από το 16ο αιώνα αλλά επιβλήθηκε το 19ο αιώνα.
Tα προβλήματα των κουρδισμάτων αφορούν περισσότερο τα πληκτροφόρα, οι μουσικοί των οποίων δεν μπορούν να επέμβουν στο ακριβές τονικό ύψος κάθε νότας.
Έτσι για να πάρουμε την καθαρή πέμπτη (το διάστημα μεταξύ Α και Ε) πρέπει να πολλαπλασιάσουμε 1,5 φορά τη συχνότητα της Α.
Στο βιολί (τη βιόλα ,τη λύρα αλλά και σ’ όλα τα χωρίς τα έγχορδα χωρίς χωρίσματα-όπως τα χωρίσματα-frets- της κιθάρας)αυτό είναι δυνατόν και μπορούμε να παίξουμε την καθαρή πέμπτη Ε στη συχνότητα 440Χ1,5=660 Hz.
Από τον παρακάτω όμως πίνακα συχνοτήτων βλέπουμε ότι το πιάνο παίζει την ίδια νότα Ε = 659.26 Hz δηλαδή να βαίνει προς ύφεση.
{ Αυτό οφείλεται στον κούρδισμα equal tempered. Λέγεται ότι το κούρδισμα αυτό επινοήθηκε ή ότι καθιερώθηκε την εποχή του Bach και πως ο Bach το προτιμούσε και το επέβαλε ή ότι βοήθησε στην καθιέρωσή του. Άλλοι λένε αυτό δεν ευσταθεί και είναι παρεξήγηση….}.
Στο Ε.Τ η οκτάβα χωρίζεται σε δώδεκα ίσα τμήματα, καθένα από τα οποία είναι “κατά προσέγγιση ένα ημιτόνιο” (λέμε κατά προσέγγιση, διότι το πραγματικό ημιτόνιο δεν είναι το ένα δωδέκατο της οκτάβας). Σύμφωνα με τον Kirnberger (μαθητή του Bach) “ο ισοσυγκερασμός δεν εξασφαλίζει την ποικιλομορφία των τονικοτήτων.
Αυτό σημαίνει ότι όλα τα παραπάνω αναφερθέντα έγχορδα πρέπει να υπακούουν σ’ αυτές τις ελαφρές διαφορές κατά τα κουρδίσματα με το πιάνο.
Οι οργανοπαίχτες αυτών των οργάνων αισθάνονται πιο ‘ευτυχείς’ όταν παίζουν μόνο με άλλα τέτοια έγχορδα.
Για καλύτερη κατανόηση του παραπάνω πίνακα συχνοτήτων δείτε ΕΔΩ:
http://www.box.net/shared/6acbbehivova368faga0
Συχνότητες των τόνων
Οι συχνότητες των τόνων βρίσκονται από τον μαθηματικό τύπο:
Συχνότητα: f= 440×12η ρίζα του 2 εις την x δύναμη
Όπου x = -21, -19, ..., 27. (το πρόσημο είναι + για πάνω από τη Α4 και – για κάτω από τη Α4). (αν αναφερόμαστε για την 1η οκτάβα ,όπως στο ανωτέρω link τότε χ=12)
Δείτε την ονομασία και τις συχνότητες των οκτάβων ΕΔΩ:
http://www.box.net/shared/yum71z5jidjjqmhesdm9
Παράδειγμα 1ον:Ποια είναι η συχνότητα του C5;
Το C5 είναι το πρώτο C πάνω από τη Α4. Ανάμεσα στο Α4 και στο C5 υπάρχουν 3 ημιτόνια (Α4 Α#4 Β4 C5 ) και η C5 πάνω από τη A4. Άρα n=+3.Αποτέλεσμα f=523,2 Hz
Παράδειγμα 2ον: Ποια είναι η συχνότητα του F4;
Το F4 είναι κάτω από το A4. Ανάμεσα στο Α4 και στο F4 υπάρχουν 4 ημιτόνια ( A4 Ab4G4Gb4F4) και άρα n=-4
Αποτέλεσμα f=349,2 Hz:
Τον πίνακα με όλες τις συχνότητες δείτε τον ΕΔΩ:
http://www.box.net/shared/gvkohn0e9d2ggas66vag
Από τον πίνακα φαίνεται ότι η οκτάβα χωρίστηκε σε 12 ίσα διαστήματα με την πρώτη και την τελευταία νότα να έχουν λόγο συχνοτήτων 2 και άρα να δίνουν το ίδιο τονικό ύψος σε διαδοχικές οκτάβες.
Εδώ : http://www.contrabass.com/pages/frequency.html
θα δείτε έναν ενδιαφέροντα πίνακα με τις νότες από C2 έως C6 τις συχνότητες τους , την περιοχή τους στα μουσικά όργανα και links σε όλα τα μουσικά όργανα για περισσότερες πληροφορίες.
Συνεχίζεται...